2の8乗をすばやくカンタンに暗算する方法

「2の8乗は？」と聞かれた時、暗記している人は「256」とすぐに答えられますが、大体の人は「えっと……」となるかと思います。

こういう時、「2が8個あるから4が4個で……」と、分裂させて計算させていくと、頭の中だけですばやくカンタンに計算できます。以下、図を交えて紹介します。

2の8乗をスピーディに解く方法

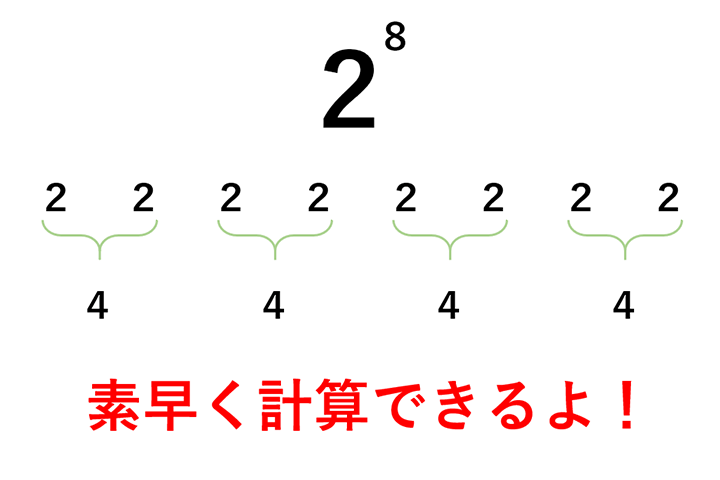
まず、「2の8乗は？」と聞かれたら、頭の中に「2」を8個、思い浮かべて見てください。

これを1個ずつ掛け算していくと苦痛ですが、しかし、「ニニンがシ（2*2=4）」の計算はとてもラクですよね。というわけで、「ニニンがシ」をすべてやっちゃいます。

で、2が8個ですので、「ニニンがシ」をやると、「4」が4個になることがわかります。

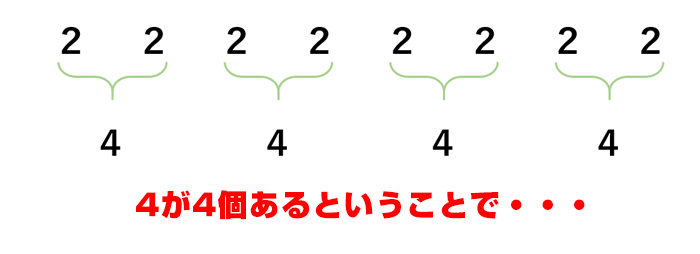
同じ要領で、「シシ、ジュウロク（4*4=16）」になりますので、「4が4個」＝「16が2個」と変換できるわけです。あとは16*16=256とするだけです。

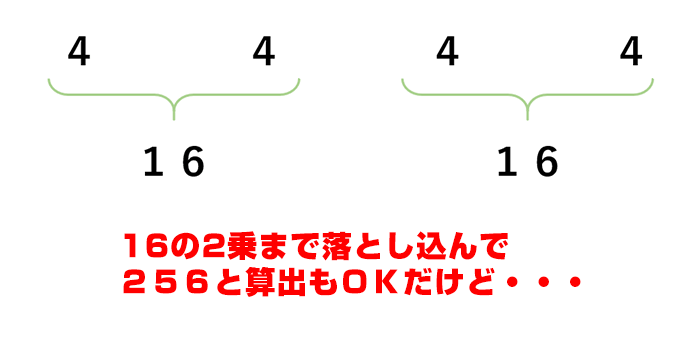
ただ、16*16は普通の人にはちょっと計算が大変かもしれませんので、そういう場合は、計算の道のりを少し変えてあげるだけでカンタンになります。

64*4=256なら、けっこうカンタンにできるかと思いますが、どうでしょう。

2の7乗は、2が7個なので、

「2 2 2 2 2 2 2」
↓
「4 4 4 2」
↓
「16 8」
↓
「128」

というように求められます。

たとえば3の7乗であれば、

「3 3 3 3 3 3 3」
↓
「9 9 9 3」
↓
「81 27」
↓
……。

うん。

いやですね。自分は瞬時に分かるんですけど、きっと普通の方にはちょっと辛いですね。（精一杯の虚言

ただまあ、ざっくり、80*30と書き換えて、2400ぐらいの大きさだなってくらい分かれば、いざという時に便利だとは思います。

進数の乗数計算は、このように数字を分裂させて計算してみると、ちょっとした数までなら、頭の中でカンタンに算出可能です。

ＩＴ・web系だと、けっこう2の●乗とか使うことも多いと思うので、いざという時は覚えておくと便利です。（暗記したほうが早いとは思いますが……。）