2直線の交点座標を連立方程式で求める方法【図解で超カンタンまとめ】
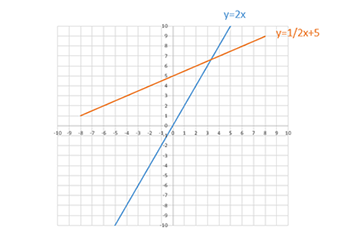
先日、ふと中学生の子どもへ、数学の1次関数を教える機会があり、交点座標が、どうして連立方程式で求められるか聞かれたので、ブログでもまとめてみました。これから座標の勉強をされる学生さんの参考になればとおもいます。
目次
2直線の交点座標がどうして連立方程式で求められるか、図解で超カンタンにまとめてみた。
例題)y=2xとy=1/2x+5の交点座標を求めてみましょう。
試しに、y=2xとy=1/2x+5の交点座標を求めてみましょう。
まず、グラフを書いてみると、こんな感じになります。
①y=2x
②y=1/2x+5
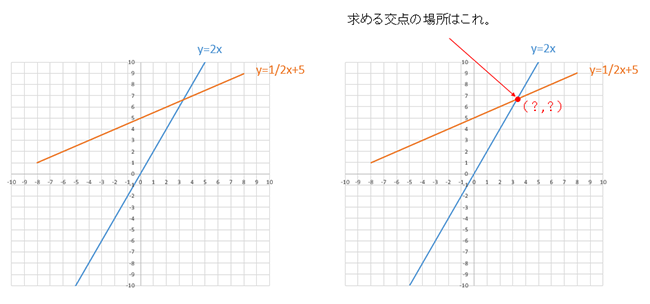
試しに、交点の(?、?)を変数に置き換えて(m,n)と仮定してみましょう。
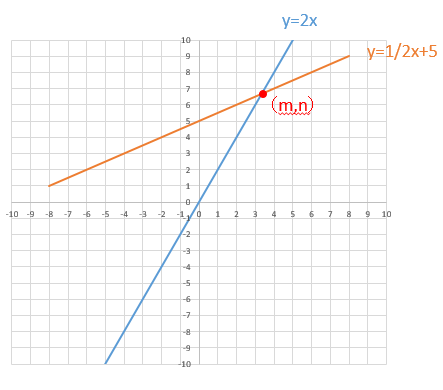
この時、①、②、どちらの式も(m,n)を通っていますので、x=m,y=nを代入してみると、、、
①n=2m
②n=1/2m+5
そして、m,nは交点座標を示したものですので、①、②はどちらの答えも同じになります。すなわち、連立方程式が使えるということです。
m,nについて、解いてみます。
①n=2m
②n=1/2m+5
2m=1/2m+5
↓
2m-1/2m=5
↓
4/2m-1/2m=5
↓
3/2m=5
↓
m=10/3
①n=2mに「m=10/3」を代入すると、「n=20/3」の答えが得られます。
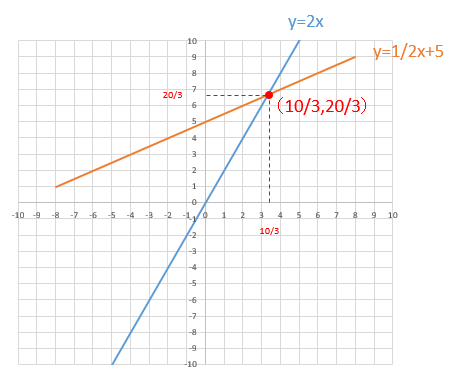
つまり、交点(m,n)の正体は(10/3,20/3)だったことが分かります!
ショートカットの計算方法
今回、交点座標を(m,n)に置き換えて考えましたが、計算上、置き換えないで、xとyのまま連立方程式で解いても一緒です。そのため、交点座標の問題が出た時は、とにかく連立方程式で解くと覚えておけばOKです!(なぜ連立方程式で解けるのか迷ったら、m,nに置換すれば同じ計算になるため、と覚えておきましょう!)

まとめ
いかがでしたでょうか。ぜひ、交点座標を連立方程式で解く際に参考にしてもらえればと思います!