応用情報の逆ポーランド記述法(後置記法)をカンタン解説します

応用情報技術者試験の勉強をすると基礎理論単元に出てくる問題の一つが、逆ポーランド記述法(後置記法)です。
ほとんどの人は見たことも聞いたこともない感じですが、ただ問題を解くだけであれば、とてもカンタンなので、図解も交えて、わかりやすく説明したいと思います。
目次
逆ポーランド記述法(後置記法)の解き方
サンプル問題
一つ問題を見てみましょう。
後置換記法(逆ポーランド表記法)では,例えば,式 Y=(A-B)×C を YAB-C×= と表現する。
次の式を後置換記法で表現したものはどれか。Y=(A+B)×(C-(D÷E))
これを逆ポーランド記述法(後置記法)で導いた答えはこちら。
YAB+CDE÷-×=
解き方を知らないと、「は?」となってしまいますが、きちんと途中式を読めば、なんとなく解き方は分かってしまいます。
途中式を見れば解き方がよくわかる
要点は、「文字合体して、符号後ろに回す」ってだけです。
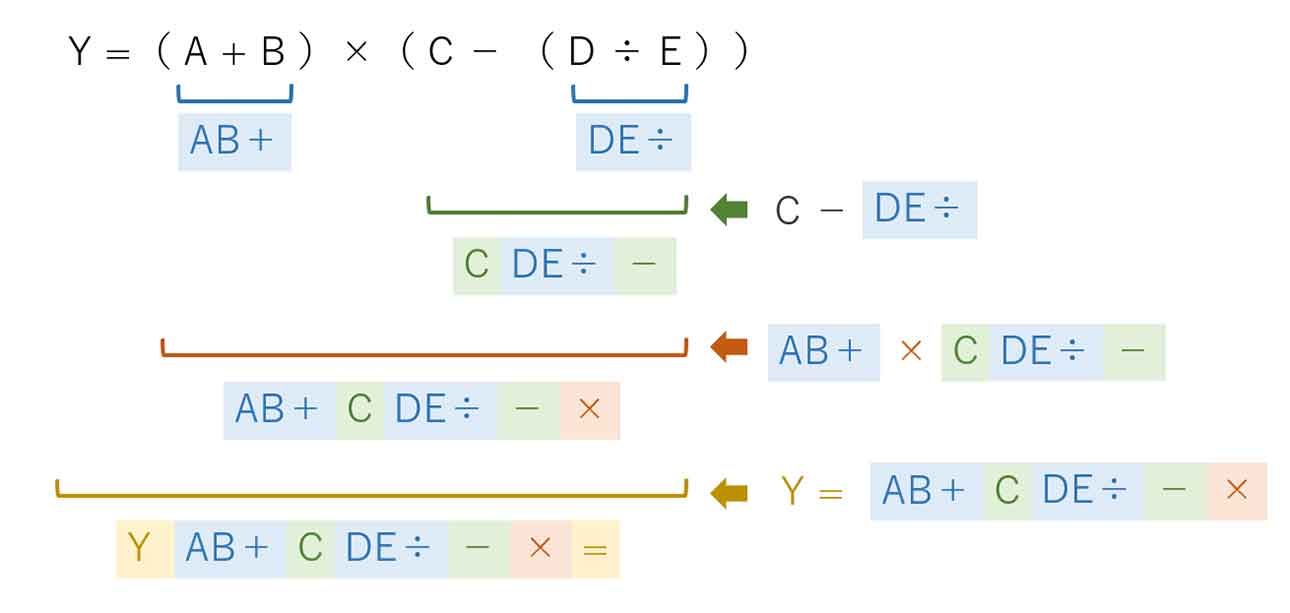
- 問題の解説
-
まずは、通常の四則演算みたいに、数式内の優先部分から計算します。
青色の「AB+」と「DE÷」が算出できたら、「AB+」と「DE÷」を一つのまとまった文字みたいに扱う感覚を持ちましょう。(一文字に置換する。)
なので、「C-DE÷」は「C-「DE÷」」という感じにして、これを逆ポーランド記述法にすれば、「C「DE÷」-」となって「CDE÷-」です。
以下、同様に処理していくと、答えを導くことができます。
文字合体して、符号後ろに回すだけ。大事なことなので、2回言っておきました!
数学というよりパズルの感覚
やり方を見るとわかるのですが、通常の数学みたいに、べつに難しい方程式や四則演算など一切いりません。
ただ、文字列と符号を並び変えて整理してあげるだけです。
そして、この時に気づいて欲しいことは、このようにパズルで遊ぶ感覚の計算というのは、まるでビット演算みたいな機械が好きそうな計算方法、ということです。
逆ポーランド記述法(後置記法)って何なの?
wikipediaの引用文では、こんな感じで解説されています。
逆ポーランド記法を使えば、式の計算をする(評価)には、先頭からひとつずつ順番に記号を読み込み、その記号が演算子以外であればスタックに値を積み、演算子であればスタックから値を取り出して演算し結果をスタックに積む、という簡単な操作の繰り返しだけでよい。そのため、プログラミング初心者の練習課題として、逆ポーランド記法の電卓を作ることがよく行われる。
プログラムでコンパイルする時、算術式を機械語に変換する過程で用いる算術式の内部表現、といった感じです。先ほどのパズル計算みたいに処理できるので、機械としても計算がラクちんなんですね。
詳しい解説動画があります
文章で分かりにくい方は、Youtube「まさるの勉強部屋」で、とてもわかりやすく解説してくれています。(むしろ、これを見るだけでOKとも思うくらい、素晴らしい動画です。)
まとめ
逆ポーランド記述法(後置記法)では、数学の難しい計算は必要ありません。
文字と符号を並び替えるだけの問題です。
正直、応用情報技術者試験で出題された時は、ただのチャンス問題です。難しい問題の多い基礎理論範囲の中で、逆ポーランド記述法(後置記法)はイージー問題です。解法を覚えて、確実に得点源となるようにしましょう。
